Số nguyên là gì? Đây là một khái niệm vô cùng quen thuộc đối với bất kỳ học sinh nào. Tuy nhiên, bạn đã thực sự hiểu được ý nghĩa của khái niệm này chưa? Hãy cùng johnwcooper.com tìm hiểu về khái niệm này trong bài viết dưới đây nhé!
I. Số nguyên là gì?
Số nguyên là một trong những khái niệm cơ bản nhất trong toán học. Số nguyên bao gồm các số nguyên dương mà nghịch đảo của chúng là các số nguyên âm. Ngoài ra, số nguyên còn bao gồm cả số 0. Đây là số duy nhất ở giữa và là ranh giới phân biệt giữa đầu dương và đầu âm.
Nếu phát biểu theo khái niệm toán học: Số nguyên là một trường số nguyên bao gồm các số được sắp xếp theo một thứ tự duy nhất. Các yếu tố tích cực của nó được sắp xếp theo một trật tự hợp lý, và các quy tắc được bảo toàn bằng cách bổ sung. Một cách đơn giản và dễ hiểu hơn để nói rằng số nguyên là số có thể được biểu thị mà không sử dụng các phần của phân số.
II. Tập hợp số nguyên Z

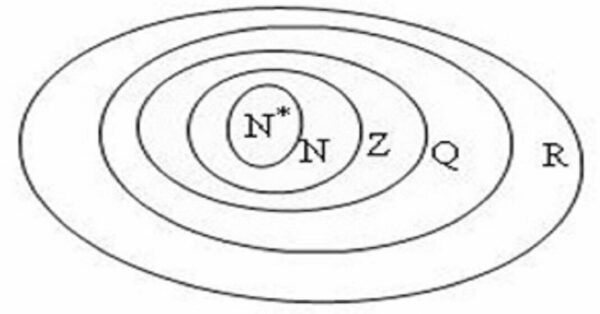
Các tập hợp số nguyên được ký hiệu bằng chữ Z. Biểu tượng này đại diện cho từ Zahl trong tiếng Đức, có nghĩa là số. Nó cũng là một tập hợp con của hai tập hợp lớn hơn, tập hợp các số hữu tỉ Q và tập số thực R. Nó cũng là tập hợp mẹ của các số tự nhiên N. và có các tính chất giống như tập hợp các số tự nhiên, số tập Z là vô hạn nhưng đếm được.
Tập hợp số nguyên Z có thể được chia thành hai tập con, Z và Z- tại đó:
- Z+ là tập hợp các nguyên dương lớn hơn 0
- Z- là tập hợp các số nguyên âm nhỏ hơn 0
- Một lưu ý là số 0 chỉ nằm trong tập hợp Z, không nằm trong hai tập con Z+ và Z-.
III. Tính chất của tập Z
- Không có khái niệm số nguyên lớn nhất và nhỏ nhất. Các khái niệm về giá trị lớn nhất và nhỏ nhất chỉ mang tính chất tương đối và phụ thuộc vào điều kiện của từng trường hợp.
- Số nguyên dương nhỏ nhất là 1. Số nguyên âm lớn nhất là -1.
- Số nguyên Z gồm vô số tập con hữu hạn. Các tập con này sẽ có các số nguyên tối thiểu và tối đa được xác định.
- Không có số nguyên nào nằm giữa hai số nguyên liên tiếp.
IV. Các tập hợp số cơ bản khác

1. Tập hợp các số tự nhiên N
N là viết tắt của tập hợp các số tự nhiên và là tập cơ sở nhỏ nhất trong một tập hợp. Số tự nhiên bao gồm các số 0, 1, 2, 3, …. Các số này được phát hiện và sử dụng để đếm, ghi và lưu trữ thông tin. Đây là bộ số đầu tiên được hình thành trong lịch sử loài người. Khái niệm về các con số đã xuất hiện trên thế giới từ rất lâu, bắt đầu từ các thời đại văn hóa cổ đại như Babylon hay Ai Cập. Tuy nhiên, khái niệm tập hợp các số tự nhiên đã không xuất hiện trong thời hiện đại cho đến thế kỷ 19, và N là tập hợp đầu tiên hình thành cơ sở của lĩnh vực lý thuyết tập hợp và khoa học máy tính.
2. Tập hợp hữu tỉ Q
Q là tập hợp các số hữu tỉ – miễn là a và b đều là số nguyên và b0, chúng có thể được biểu diễn dưới dạng các số với phân số a/ b. Q, giống như N hoặc Z, là một tập hợp vô hạn nhưng có thể đếm được. Một số hữu tỉ có thể được biểu diễn bằng nhiều phân số khác nhau và dưới dạng số thập phân. Số hữu tỉ ở dạng thập phân có thể trở thành số thập phân tuần hoàn hoặc số thập phân tuần hoàn.
3. Tập hợp các số vô tỉ I
I là một tập hợp các số vô tỉ — các số không thể biểu diễn dưới dạng phân số. Số vô tỉ thường được hiểu là số thực không phải là số hữu tỉ. Người đầu tiên đặt câu hỏi về sự tồn tại của số vô tỉ là một nhà toán học Pitago. Ông đã phát hiện ra vấn đề này khi cố gắng sử dụng phương pháp Pitago để xác định độ dài cạnh của ngôi sao năm cánh. Phải có một đơn vị độ lớn đủ nhỏ để biểu thị độ dài cạnh của ngôi sao và con số không thể được biểu thị bằng tỷ số của hai số nguyên.
4. Tập hợp các số thực
R là một tập hợp các số thực, được định nghĩa là một khái niệm lớn bao gồm các khái niệm về số tự nhiên, số nguyên, số hữu tỉ và số vô tỉ. Đây là bộ số lớn nhất và được coi là một hệ đại số khổng lồ. Ngoại trừ số 0 ở tâm trục, bất kỳ số thực nào khác đều là số âm hoặc số dương. Về bản chất, R, giống như bất kỳ tập hợp con nào khác, là một tập hợp vô hạn các số. Tuy nhiên, kích thước của tập hợp này quá lớn nên số lượng số thực là không thể đếm được.
5. Tập hợp phức C
C là tập hợp các số phức có dạng a bi, trong đó a, b là các số thực và i là đơn vị của các số ảo. Do cách biểu diễn này, số phức sẽ bao gồm hai phần là phần thực và phần ảo. Cha đẻ của khái niệm số học này là nhà toán học người Ý ở thế kỷ 14 Gerolamo Cardano, người có ứng dụng đầu tiên là giải các phương trình bậc ba. Kể từ đó, số phức được sử dụng để giải các bài toán không có lời giải thực. Đây là một khái niệm được sử dụng trong nhiều lĩnh vực khoa học khác nhau, chẳng hạn như lý thuyết hỗn loạn trong khoa học kỹ thuật, điện từ học, cơ học, vật lý lượng tử và toán học ứng dụng.
Trên đây là bài viết giới thiệu về số nguyên là gì cùng các thuộc tính của số nguyên. Hy vọng qua bài viết này bạn đọc đã có thêm nhiều kiến thức thú vị về số nguyên nhé!
