Toán học là một trong những môn học bắt buộc đối với mỗi học sinh Việt Nam từ bậc tiểu học đến khi tốt nghiệp THPT. Kiến thức về toán học luôn là vô tận và vô cùng phong phú. Bài viết này sẽ giúp bạn trả lời tất cả các câu hỏi về số thực là gì, ví dụ về số thực và các tính chất của chúng. Mời bạn đọc cùng tìm hiểu nhé!
I. Số thực là gì?

- Số thực là một số được xác định bởi các thành phần của chính nó. Tập hợp các số thực được coi là hợp của tập hợp các số vô tỉ và tập hợp các số hữu tỉ. Số thực này có thể là đại số hoặc siêu việt. Tập hợp thực được đặt làm đối chứng của tập hợp phức tạp. Các con số thực được mô tả một cách không chính thức theo nhiều cách khác nhau. Số thực thường bao gồm số dương, số 0 và số âm.
- Trong toán học, một số thực là giá trị của một đại lượng liên tục, được biểu thị bằng khoảng cách dọc theo đường thẳng. Tính từ số thực này được giới thiệu vào thế kỷ 17 bởi nhà toán học người Pháp René Descartes, người đã phân biệt giữa các căn thức thực và ảo của đa thức.
- Số thực sẽ bao gồm tất cả các số hữu tỉ, bao gồm cả số nguyên và số thập phân. Ví dụ, số nguyên -5, phân số 4/3 và tất cả các số vô tỉ, chẳng hạn như: √2 (1.41421356 …, căn bậc hai của 2, số đại số vô tỉ). Có những số siêu việt trong số vô tỉ, chẳng hạn như π (3,14159256 …). Ngoài việc đo khoảng cách, số thực còn được dùng để đo các đại lượng khác như thời gian, năng lượng, khối lượng, tốc độ,…
- Về bản chất, tập hợp các số thực là vô hạn và không đếm được. Tức là khi tập hợp các số tự nhiên và mọi tập hợp các số thực là vô hạn. Không thể có một hàm duy nhất từ số thực thành số tự nhiên và lực của tập tất cả các số thực thường lớn hơn nhiều so với tập tất cả các số tự nhiên.
- Tập hợp các số thực được ký hiệu là R.
II. Tính chất của số thực
- Bất kỳ số thực nào khác 0 đều là số âm hoặc số dương.
- Tích của hai số thực không âm cũng là một số thực không âm. Điều này có nghĩa là chúng được đóng trong các hoạt động này và tạo thành một vòng tích cực. Từ đó nó tạo ra một chuỗi số thực tuyến tính dọc theo trục số.
- Các số thực sẽ tạo thành một tập hợp vô hạn các số, thay vì chỉ phản ánh một tập hợp vô hạn các số tự nhiên. Điều này chứng tỏ rằng có nhiều số thực hơn bất kỳ phần tử nào khác trong một tập hợp đếm được.
- Số thực được sử dụng cho các phép đo đại lượng liên tục. Chúng có thể được hiển thị bằng cách sử dụng các biểu diễn thập phân, hầu hết chúng có một dãy số vô hạn ở bên phải của dấu thập phân, thường được biểu diễn dưới dạng: 324.832122147…. Dấu chấm lửng cho biết vẫn còn nhiều số nữa xuất hiện.
III. Các thuộc tính của số thực
Số thực có hai thuộc tính cơ bản: thuộc tính trường có thứ tự và thuộc tính giới hạn trên tối thiểu.
- Thuộc tính trường có thứ tự: Thuộc tính này chỉ ra rằng một số thực bao gồm một trường, bao gồm phép cộng và phép nhân với phép cộng và phép chia số khác không. Chúng có thể được sắp xếp đầy đủ trên trục số ngang theo cách tương thích với phép cộng và phép nhân.
- Thuộc tính của giới hạn trên thấp nhất: Thuộc tính này chỉ ra rằng nếu một tập hợp các số thực không rỗng có giới hạn trên thì nó có giới hạn trên bao gồm các số thực nhỏ nhất.
IV. Các dạng bài tập toán thường gặp liên quan đến số thực
1. Các câu hỏi về bài tập hợp số
Phương pháp sử dụng: Sử dụng các ký hiệu về tập hợp số. Trong đó:
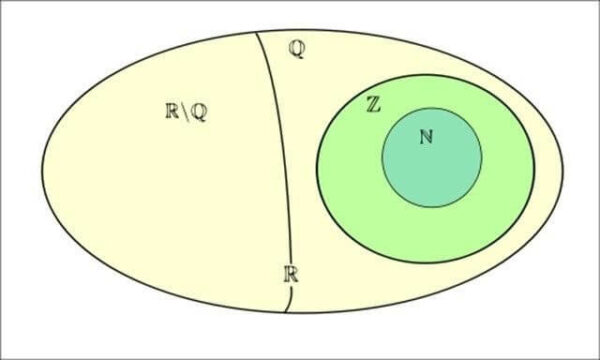
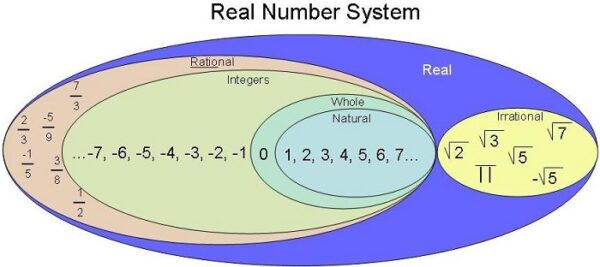
- N: Tập hợp các số tự nhiên
- Z: Tập hợp các số nguyên
- Q: Tập hợp các số hữu tỉ
- I: là tập hợp các số vô tỉ
- R: là tập hợp các số thực
Ta có quan hệ giữa các tập hợp số như sau: N ⊂ Z ⊂ Q ⊂ R; I ⊂ R.
2. Tìm số chưa biết trong một đẳng thức
Phương pháp sử dụng:
- Sử dụng thuộc tính từ của hành động.
- Sử dụng mối quan hệ giữa các khoản mục tổng và hiệu; mối quan hệ giữa các tính năng trong một sản phẩm; mối quan hệ giữa số bị chia, số bị chia và thương trong phép chia.
- Sử dụng quy tắc chuyển đổi để ngắt dấu ngoặc đơn.
3. Tính giá trị của biểu thức nào đó
Phương pháp sử dụng:
- Thực hiện các phép tính cộng, trừ, nhân, chia, lũy thừa. Chú ý đến thứ tự thực hiện: nhân chia trước, cộng trừ sau.
- Rát gọn các phân số khi cần.
- Vận dụng các đặc điểm của phép toán một cách hợp lý.
Với những thông tin mà johnwcooper.com chia sẻ trên đây hy vọng đã giúp bạn đọc nắm được khái niệm số thực là gì? Tính chất, thuộc tính và các dạng bài tập toán thường gặp liên quan đến số thực nhé!
